TUGAS STATISTIK : KOEFISIEN KORELASI
Nama : Ulan Juniarti
NIM : 210112006
Prodi : Sistem Informasi
Manfaat Korelasi
Jenis-Jenis Korelasi
Bentuk Hubungan Korelasi
Korelasi Pearson adalah alat analisis statistik yang digunakan untuk melihat keeratan hubungan linier antara 2 variabel yang skala datanya adalah interval atau rasio.
Rumus yang dapat digunakan untuk menghitung koefisien korelasi Pearson (r) adalah sebagia berikut:
Nilai terletak antara – 1 sampai 1 .
Jika berarti antara variabel X dan Y terdapat hubungan linier (garis lurus) yang negatif (berlawanan arah , jika nilai variabel X bertambah besar maka nilai variabel Y akan bertambah kecil, dan sebaliknya jika nilai variabel X bertambah kecil maka nilai variabel Y akan bertambah besar) dan sempurna (semua pasangan nilai X, Y berada pada suatu garis lurus).
Jika berarti tidak ada hubungan garis lurus antara variabel X dan Y. Akan tetapi, mungkin saja antara X dan Y terdapat hubungan yang berbentuk bukan garis lurus, misalnya hubungan kuadratik.
Jika berarti antara variabel X dan variabel Y terdapat hubungan linier (garis lurus) yang positif (searah, yaitu jika nilai variabel X bertambah besar maka nilai variabel Y akan bertambah besar, dan demikian juga jika nilai variabel X bertambah kecil maka nilai variabel Y akan bertambah kecil) dan sempurna (semua pasangan nilai X, Y berada pada garis lurus).
contoh
Berdasarkan data berikut (diperoleh dari pasangan data X dan Y), hitunglah koefisien korelasi antara X dan Y!
Pembahasan
Berdasarkan data di atas, koefisien korelasi dari ke dua variabel tersebut adalah:
Koefisien korelasi yang diperoleh menunjukkan bahwa ada hubungan negatif (berlawanan arah) yang kuat antara variabel X dengan variabel Y.
B. Korelasi Kendall
Secara umum, uji korelasi Kendall adalah salah satu bagian dari uji statistik non-parametric. Artinya, dalam proses pengujian ini, nantinya tidak ada asumsi atau sebuah pernyataan khusus yang mewajibkan bahwa data penelitian harus terdistribusi dengan normal. Selain itu, tidak ada pula keharusan di mana hubungan yang terbentuk dari variable harus linear.
Dari beberapa pernyataan di atas, bisa disimpulkan jika dalam uji korelasi Kendall ini, data penelitian yang digunakan boleh saja tidak normal ataupun tidak linear. Hal ini cukup berbeda dengan uji statistik parametric di mana ada persyaratan terkait data yang cenderung harus terdistribusi normal dan juga linear.
Rumus yang digunakan untuk mengukur koefisien korelasi kendall adalah:
Keterangan:
S: statistik untuk jumlah konkordansi dan diskordansi
n: jumlah pasangan X dan Y
Contoh :
Diketahui sebuah ranking nilai wawancara dari dua orang pewawancara kepada 10 orang peserta dari tes tertulis dan tes praktek. Data nilai ranking sebagai berikut:
Apakah ada hubungan ranking penilaian dari pewawancara 1 dan pewawancara 2? Gunakan tingkat signifikansi 5%.
Pembahasan:
Hipotesis:
H0: Tidak ada kesesuaian ranking nilai pewawancara 1 dan pewawancara 2
H1: Ada kesesuaian ranking nilai pewawancara 1 dan pewawancara 2
Tingkat signifikansi (alpha = 0,05)
Statistik uji
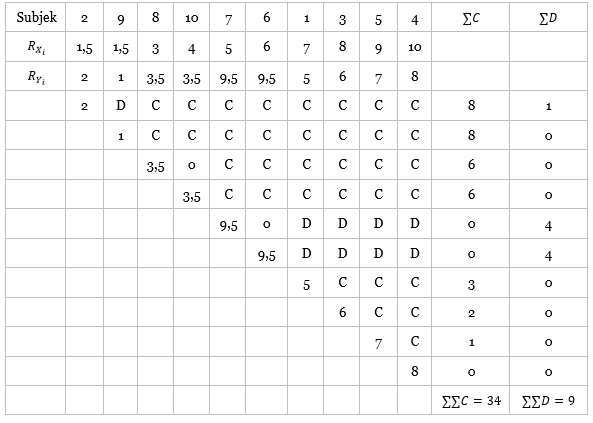
Ranking berdasarkan urutan pewawancara 1
Sesudah mengatur ranking-ranking itu, dengan dasar ranking dari pewawancara 1, kita tetapkan harga S untuk ranking yang saling berhubungan dengan variabel Y sehingga diperoleh nilai S sebesar 25.
Karena terdapat ranking kembar, maka gunakan rumus korelasi kendall tau dengan faktor koreksi. Pertama kita hitung dulu yang berikut ini.
Dengan demikian, kita peroleh
Pada tabel kendall tau untuk nilai S = 25 dan n = 10 diperoleh nilai τ tabel = 0,014. Karena nilai τ hitung > τ tabel, maka tolak Ho pada tingkat signifikansi α=5%.
Kesimpulan: Dengan tingkat signifikansi 5%, terdapat cukup bukti untuk mengatakan bahwa ada kesesuaian ranking nilai pewawancara 1 dan pewawancara 2 di tingkat populasi.
C. Korelasi Spearman
Korelasi Spearman atau sering disebut juga sebagai Spearman Rank Correlation Coefficient, digunakan untuk menghitung korelasi berdasarkan data yang berbentuk peringkat (ranking). Berdasarkan kondisi dalam data, terdapat dua metode dalam penghitungan koefisien korelasi Spearman, yaitu:
- Apabila tidak terdapat peringkat yang “kembar/sama” (“tied rank”). Rumus yang digunakan untuk menghitung korelasi Spearman tanpa peringka sama adalah
- Apabila terdapat peringkat yang “kembar/sama” (“tied rank”). Rumus yang digunakan jika terdapat ranking kembar yaitu


Keterangan:
contoh :
Seorang manager produksi ingin mengetahui apakah ada hubungan antara nilai tes bakat (aptitude test)
pada waktu penerimaan kerja dengan rating tampilannya setelah satu semester bekerja. Nilai aptitude
test berkisar antara 0 sampai 100. Sedangkan rating tampilan mempunyai skala sebagai berikut:
1 =
pekerja berpenampilan sangat dibawah rata-rata
2 =
pekerja berpenampilan dibawah rata-rata
3 =
pekerja berpenampilan sedang (rata-rata)
4 =
pekerja berpenampilan diatas rata-rata
5 = pekerja berpenampilan sangat diatas rata-rata




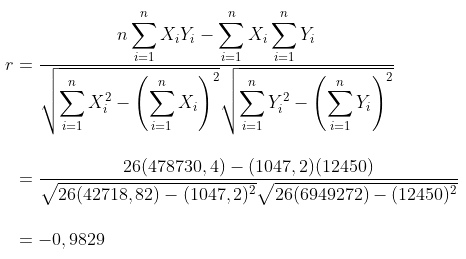










Komentar
Posting Komentar